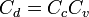martes, 3 de noviembre de 2015

GASTOS VOLUMETRICOS, TEOREMA DE BERNOULLI Y SUS APLICACIONES, EDUCACION DE CONTINUIDAD

Gasto o Caudal

  • En dinámica de fluidos, caudal es la cantidad de fluido que avanza en una unidad de tiempo. Se denomina también caudal volumétrico o índice de flujo fluido, y que puede ser expresado en masa o en volumen. Caudalímetro: instrumento empleado para la medición del caudal de un fluido o gasto másico.Cálculo de caudal de agua en tubería: estimación del comportamiento de un flujo de tubería, basado en la ecuación de continuidad:En ecología, se denomina caudal al volumen de agua que arrastra un río, o cualquier otra corriente de agua para preservar los valores ecológicos en el cauce de la misma; se mide en metros cúbicos por segundo.
Asociado al término anterior:
  • Caudal sólido: denominación para el material arrastrado por la corriente de agua.
  • Caudal regularizado: determinación de la capacidad reguladora de un embalse.
  • Régimen fluvial: se refiere a las variaciones en el caudal de un río a lo largo de un año.
La ecuación de continuidad se puede expresar como:
ρ1.A1.V1 = ρ2.A2.V2
Cuando ρ1 = ρ2, que es el caso general tratándose de agua, y flujo en régimen permanente, se tiene:
[pic]
o de otra forma:
[pic](el caudal que entra es igual al que sale)
Donde:
• Q = caudal (metro cúbico por segundo; m3 / s)
• V = velocidad (m / s)
• A = area transversal del tubo de corriente o conducto (m2)

 

TEOREMA DE  DANIEL BERNOULLI

El principio de Bernoulli, también denominado ecuación de Bernoulli o Trinomio de Bernoulli, describe el comportamiento de un fluido en reposo moviéndose a lo largo de una corriente de agua. Fue expuesto por Daniel Bernoulli en su obra Hidrodinámica (1738) y expresa que en un fluido ideal (sin viscosidad ni rozamiento) en régimen de circulación por un conducto cerrado, la energía que posee el fluido permanece constante a lo largo de su recorrido. La energía de un fluido en cualquier momento consta de tres componentes:

  1. Cinética: es la energía debida a la velocidad que posea el fluido.

  2. Potencial gravitacional: es la energía debido a la altitud que un fluido posea.

  3. Energía de flujo: es la energía que un fluido contiene debido a la presión que posee.

La siguiente ecuación conocida como “Ecuación de Bernoulli” (Trinomio de Bernoulli) consta de estos mismos términos.


<br /><br /><br /><br /><br /> \frac{V^2 \rho}{2}+{P}+{\rho g z}=constante<br /><br /><br /><br /><br />

donde:

  • V= velocidad del fluido en la sección considerada.

  • \rho = densidad del fluido.

  • P = presión a lo largo de la línea de corriente.

  • g = aceleración gravitatoria

  • z = altura en la dirección de la gravedad desde una cota de referencia.

Para aplicar la ecuación se deben realizar los siguientes supuestos:

  • Viscosidad (fricción interna) = 0 Es decir, se considera que la línea de corriente sobre la cual se aplica se encuentra en una zona ‘no viscosa’ del fluido.

  • Caudal constante

  • Flujo incompresible, donde ρ es constante.

  • La ecuación se aplica a lo largo de una línea de corriente o en un flujo rotacional

Aunque el nombre de la ecuación se debe a Bernoulli, la forma arriba expuesta fue presentada en primer lugar por Leonhard Euler.

Un ejemplo de aplicación del principio lo encontramos en el flujo de agua en tubería.

Cada uno de los términos de esta ecuación tiene unidades de longitud, y a la vez representan formas distintas de energía; en hidráulica es común expresar la energía en términos de longitud, y se habla de altura o cabezal, esta última traducción del inglés head. Así en la ecuación de Bernoulli los términos suelen llamarse alturas o cabezales de velocidad, de presión y cabezal hidráulico, del inglés hydraulic head; el término z se suele agrupar con P/\gamma (donde \gamma = \rho g ) para dar lugar a la llamada altura piezo métrica o también carga piezométrica.[editar]Características y consecuencia

\overbrace{{V^2 \over 2 g}}^{\mbox{cabezal de velocidad}}+\overbrace{\underbrace{\frac{P}{\gamma}}_{\mbox{cabezal de presión}} + z}^{\mbox{altura o carga piezométrica}} = \overbrace{H}^{\mbox{Cabezal o Altura hidráulica}}

También podemos reescribir este principio en forma de suma de presiones multiplicando toda la ecuación por \gamma, de esta forma el término relativo a la velocidad se llamará presión dinámica, los términos de presión y altura se agrupan en la presión estática.

Esquema del efecto Venturi.

\underbrace{\frac{\rho V^2}{2}}_{\mbox{presión dinámica}}+\overbrace{P+ \gamma z}^{\mbox{presión estática}}=constante

o escrita de otra manera más sencilla:

q+p=p_0

donde

  • q=\frac{\rho V^2}{2}

  • p=P+ \gamma z

  • p_0 es una constante-

Igualmente podemos escribir la misma ecuación como la suma de la energía cinética, la energía de flujo y la energía potencial gravitatoria por unidad de masa:

\overbrace{\frac{{V}^2}{2}}^{\mbox{energía cinética}}+\underbrace{\frac{P}{\rho}}_{\mbox{energía de flujo}}+\overbrace{g z}^{\mbox{energía potencial}} = constante

Aplicaciones del Principio de Bernoulli

Chimenea
Las chimeneas son altas para aprovechar que la velocidad del viento es más constante y elevada a mayores alturas. Cuanto más rápidamente sopla el viento sobre la boca de una chimenea, más baja es la presión y mayo

 

Tubería

La ecuación de Bernoulli y la ecuación de continuidad también nos dicen que si reducimos el área transversal de una tubería para que aumente la velocidad del fluido que pasa por ella, se reducirá la presión.  es la diferencia de presión entre la base y la boca de la chimenea, en consecuencia, los gases de combustión se extraen mejor.

Natación
La aplicación dentro de este deporte se ve reflejado directamente cuando las manos del nadador cortan el agua generando una menor presión y mayor propulsión.

Carburador de automóvil
En un carburador de automóvil, la presión del aire que pasa a través del cuerpo del carburador, disminuye cuando pasa por un estrangulamiento. Al disminuir la presión, la gasolina fluye, se vaporiza y se mezcla con la corriente de aire.

Flujo de fluido desde un tanque
La tasa de flujo está dada por la ecuación de Bernoulli.

Dispositivos de Venturi
En oxigeno terapia  la mayor parte de sistemas de suministro de débito alto utilizan dispositivos de tipo Venturi, el cual esta basado en el principio de Bernoulli.

Aviación
Los aviones tienen el extradós (parte superior del ala o plano) más curvado que el intradós (parte inferior del ala o plano). Esto causa que la masa superior de aire, al aumentar su velocidad, disminuya su presión, creando así una succión que ayuda a sustentar la aeronave.

 

 

 

Ecuación de continuidad

 

 
        

En física, una ecuación de continuidad expresa una ley de conservación de forma matemática, ya sea de forma integral como de forma diferencial.

 

 

 


TEORÍA ELECTROMAGNÉTICA

En teoría electromagnética, la ecuación de continuidad viene derivada de dos de las ecuaciones de Maxwell. Establece que la divergencia de la densidad de corriente es igual al negativo de la derivada de la densidad de carga respecto del tiempo:
En otras palabras, sólo podrá haber un flujo de corriente si la cantidad de carga varía con el paso del tiempo, ya que esta disminuye o aumenta en proporción a la carga que es usada para alimentar dicha corriente.
\nabla \cdot \vec{J} = - {\partial \rho \over \partial t}
Esta ecuación establece la conservación de la carga.

MECÁNICA DE FLUIDOS

En mecánica de fluidos, una ecuación de continuidad es una ecuación de conservación de la masa. Su forma diferencial es:
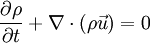
{\partial \rho \over \partial t} + \nabla \cdot (\rho \vec{u}) = 0
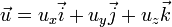donde  \rho  es la densidad, t el tiempo y \vec{u} = u_x \vec i + u_y \vec j + u_z \vec k la velocidad del fluido. Es una de las tres ecuaciones de Euler.

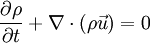
MECÁNICA CUÁNTICA

En Mecánica cuántica, una ecuación de continuidad es una ecuación de conservación de la probabilidad. Su forma diferencial es:[1]
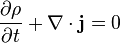
\frac {\partial \rho}{\partial t} + \nabla \cdot \mathbf{j} = 0
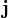Donde  \rho  es la densidad de probabilidad de la función de ondas y  \mathbf{j}  es la corriente de probabilidad o densidad de corriente. Estas dos expresiones se pueden relacionar con la función de onda de una partícula como:
\rho=|\Psi|^2=\Psi^*(\mathbf{r},t)\Psi(\mathbf{r},t), \quad \mathbf{j} = {i \over 2m} \left( \Psi^*\boldsymbol{\nabla}\Psi - \Psi\boldsymbol{\nabla}\Psi^* \right)\,\!

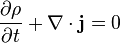
MECÁNICA RELATIVISTA

En la teoría especial de la relatividad, una ecuación de continuidad debe escribirse en forma covariante, por lo que la ecuación de continuidad usual para la carga eléctrica y otras magnitudes conservadas se suele escribir en teoría de la relatividad como:
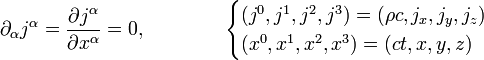
\part_\alpha j^\alpha = \frac{\part j^\alpha}{\part x^\alpha} = 0, \qquad \qquad \begin{cases} (j^0, j^1, j^2, j^3) = (\rho c, j_x, j_y, j_z)\\ (x^0,x^1,x^2,x^3) = (ct, x, y, z) \end{cases}
La ecuación de continuidad para la densidad másica (o más exactamente la energía másica) y la densidad de momento lineal se escribe en términos del tensor energía impulso:
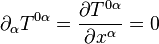
\part_\alpha T^{0\alpha} = \frac{\part T^{0\alpha}}{\part x^\alpha} = 0
En el contexto de la teoría general de la relatividad las derivadas parciales deben substituirse por derivadas covariantes:
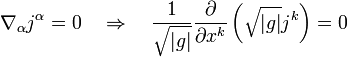
\nabla_\alpha j^\alpha = 0 \quad \Rightarrow \quad \frac{1}{\sqrt{|g|}} \frac{\part}{\part x^k} \left(\sqrt{|g|} j^k \right) = 0
Donde 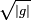\scriptstyle \sqrt{|g|} es la raíz del determinante del tensor métrico asociado a las coordenadas \scriptstyle x^\alpha. Y análogamente para la conservación de la energía:
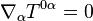
\nabla_\alpha T^{0\alpha} = 0

Publicadas por a la/s No hay comentarios.:

Teorema de Torricelli

Resultado de imagen para experimento de torricelli

   
El teorema de Torricelli o principio de Torricelli es una aplicación del principio de Bernoulli y estudia el flujo de un líquido contenido en un recipiente, a través de un pequeño orificio, bajo la acción de la gravedad.
La velocidad de un líquido en una vasija abierta, por un orificio, es la que tendría un cuerpo cualquiera, cayendo libremente en el vacío desde el nivel del líquido hasta el centro de gravedad del orificio.
Matemáticamente:
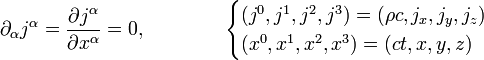
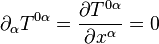
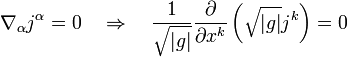
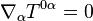
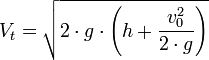
V_t = \sqrt{{2\cdot g\cdot\left ( h + \frac {v_0^2} {2\cdot g} \right ) }}
donde:
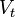  • \ V_t  es la velocidad teórica del líquido a la salida del orificio
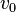  • \ v_0  es la velocidad de aproximación o inicial.
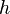  • \ h  es la distancia desde la superficie del líquido al centro del orificio.
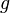  • \ g  es la aceleración de la gravedad
Para velocidades de aproximación bajas, la mayoría de los casos, la expresión anterior se transforma en:
V_r = C_v \sqrt{{2\cdot g\cdot h }}
donde:
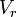  • \ V_r  es la velocidad real media del líquido a la salida del orificio
  • \ C_v  es el coeficiente de velocidad. Para cálculos preliminares en aberturas de pared delgada puede admitirse 0,95 en el caso más desfavorable.
tomando  \ C_v  =1
V_r = \sqrt{{2\cdot g\cdot h }}
Experimentalmente se ha comprobado que la velocidad media de un chorro de un orificio de pared delgada, es un poco menor que la ideal, debido a la viscosidad del fluido y otros factores tales como la tensión superficial, de ahí el significado de este coeficiente de velocidad.


El caudal o volumen del fluido que pasa por el orificio en un tiempo, \ Q, puede calcularse como el producto de \ S_c, el área real de la sección contraída, por \ V_r, la velocidad real media del fluido que pasa por esa sección, y por consiguiente se puede escribir la siguiente ecuación:
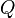
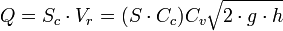
Q = S_c\cdot V_r = (S\cdot C_c)C_v\sqrt{{2\cdot g\cdot h}}
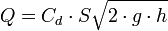
Q = C_d\cdot S\sqrt{{2\cdot g\cdot h}}
en donde
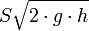  • S\sqrt{{2\cdot g\cdot h}} representa la descarga ideal que habría ocurrido si no estuvieran presentes la fricción y la contracción.
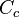  • \ C_c es el coeficiente de contracción de la vena fluida a la salida del orificio. Su significado radica en el cambio brusco de sentido que deben realizar las partículas de la pared interior próximas al orificio. Es la relación entre el área contraída 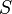\ S_c y la del orificio \ S. Suele estar en torno a 0,65.
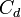  • \ C_d es el coeficiente por el cual el valor ideal de descarga es multiplicado para obtener el valor real, y se conoce como coeficiente de descarga. Numéricamente es igual al producto de los otros dos coeficientes. \ C_d=C_c C_v
El coeficiente de descarga variará con la carga y el diámetro del orificio. Sus valores para el agua han sido determinados y tabulados por numerosos experimentadores. De forma orientativa se pueden tomar valores sobre 0,6. Así se puede apreciar la importancia del uso de estos coeficientes para obtener unos resultados de caudal aceptables.
Publicadas por a la/s No hay comentarios.:
Suscribirse a: Entradas (Atom)