martes, 17 de mayo de 2016

Circuitos de primer orden RL y RC

Descripción de los circuitos


Los circuitos serie RL y RC (figura 1) tienen un comportamiento similar en cuanto a su respuesta en corriente y en tensión, respectivamente.
Al cerrar el interruptor S en el circuito serie RL, la bobina crea una fuerza electromotriz (FEM) que se opone a la corriente que circula por el circuito, denominada por ello fuerza contraelectromotriz. Como consecuencia de ello, en el mismo instante de cerrar el interruptor (t0 en la figura 2) la intensidad será nula e irá aumentando exponencialmente hasta alcanzar su valor máximo, Io = E/R (de t0 a t1). Si a continuación, en el mismo circuito abrimos S (se hará circuito abierto en la red RL),y el valor de Io no desaparecería instantáneamente, sino que iría disminuyendo de forma exponencial hasta hacerse cero (de t2 a t3).
Por otro lado, en el circuito serie RC, al cerrar el interruptor S (t0 en la figura 2), el condensador comienza a cargarse, aumentando su tensión exponencialmente hasta alcanzar su valor máximo E0 (de t0 a t1), que coincide con el valor de la FEM E de la fuente. Si a continuación, en el mismo instante de abrir S (t2 en la figura 2) se hará corto circuito en la red RC, el valor de Eo no desaparecería instantáneamente, sino que iría disminuyendo de forma exponencial hasta hacerse cero (de t2 a t3).

Régimen de Funcionamiento

En ambos circuitos se da por lo tanto dos tipos de régimen de funcionamiento (figura 2):
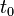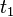  • Transitorio: desde t_0 a t_1 (carga) y desde 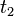t_2 a t_3 (descarga).
  • Permanente: desde 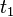t_1 a t_2.
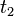La duración del régimen transitorio depende, en cada circuito, de los valores de la resistencia, R, la capacidad, C, del condensador y de la autoinductancia, L de la bobina. El valor de esta duración se suele tomar como 5 \tau , donde \tau es la denominada constante de tiempo, siendo su valor en cada circuito:
\quad \tau = \mbox{RC}
\quad \tau = {L \over R}
Si R está en ohmios, C en faradios y L en henrios, \tau estará en segundos. Matemáticamente se pueden obtener las ecuaciones en régimen transitorio de cada circuito que se muestran en la siguiente tabla:
Carga en RL Descarga en RL Carga en RC Descarga en RC
\quad i(t) = Io (1 - e^{-t \over \tau})
 \quad \mbox{t} = \tau ln {Io \over Io - i(t)} \quad i(t) = Io e^{-t \over \tau}
\quad \mbox{t} = \tau ln {Io \over i(t) }		 \quad v_c(t) = Eo (1 - e^{-t \over \tau})
 \quad \mbox{t} = \tau ln {Eo \over Eo - v_c(t)}		 \quad v_c(t) = Eo e^{-t \over \tau}
 \quad \mbox{t} = \tau ln {Eo \over v_c(t) }
Publicadas por a la/s

No hay comentarios.:

Publicar un comentario

Suscribirse a: Comentarios de la entrada (Atom)